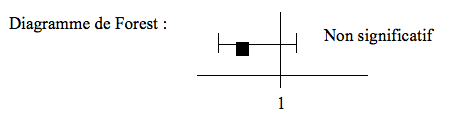Eléments de statistiques médicales
Date de dernière édition : 22/09/2024
Les statistiques permettent de manière générale de transposer une incertitude en connaissance utilisable. Bien que des résultats valables pour un grand nombre ne sont pas systématiquement transposables à tout individu (qui peut se situer aux extrêmes) auquel le médecin fait face, l'usage des statistiques en médecine est devenu le socle non seulement de la constitution des connaissances mais aussi de la pratique clinique en médecine contemporaine (Evidence Based Medicine ou Médecine Basée sur des Preuves).
Cet article n'a pas pour but de constituer un cours de statistiques (médecin est un métier, statisticien en est un autre). La réalisation des études médicales les plus simples passe par l'usage de tables pré-établies pour les différents tests statistiques ou de logiciels, les plus complexes par la collaboration avec des épidémiologistes, mieux formés aux statistiques, ou de véritables statisticiens. Face à la croissance exponentielle des publications et l'usage qui en est fait (quel médecin ne s'est-il jamais retrouvé au détour d'un couloir face à un représentant pharmaceutique lui mettant sous le nez une étude mal réalisée, dont une partie des résultats n'étaient pas significatifs ou dont des résultats significatifs n'étaient de signification que négligeable ? quel médecin n'a t-il pas été choqué par les scandales ayant aboutit à la dépublication en masse d'articles non pas simplement "erronés" mais véritablement frauduleux par des revues prestigieuses ?), tout médecin doit cependant pouvoir appréhender différents concepts lui permettant de comprendre et interpréter les résultats d'une étude médicale voire de réaliser seul des études simples.
Cet article n'a par ailleurs de sens que mis en articulation avec l'article consacré à l'épidémiologie médicale dont les éléments sont plus faciles d'accès et de plus grande importance pour la pratique clinique.
Introduction
Terminologie
Hasard signifie "jeu de dé" en arabe, traduisant un événement dont l'issue est imprévisible.
Randomisation : distribution faite au hasard.
Processus stochastique ( = aléatoire) : processus dont le résultat dépend du hasard.
Statistiques descriptives : résumé des caractéristiques propres (paramètres) à une population (ou un échantillon).
Statistiques déductives (=inférentielles) : permet de formuler des hypothèses Ho sur les paramètres d’une population. Ces hypothèses seront vérifiés sur base des paramètres d’un échantillon.
Probabilités : nombre (entre 0 = non réalisation de l’événement et 1 = réalisation certaine de l’événement) traduisant le degré de confiance dans la réalisation d’un événement = quantification de l’expression du hasard pouvant expliquer les observations. C’est le pourcentage de réalisation d’un événement si on le répétait un très grand nombre de fois dans des conditions similaires.
Probabilités subjectives (= personnelles) : degré de croyance en la survenue de l’événement. Le "sens clinique" lui correspond en médecine.
Population et échantillon :
- Population : tout groupe d’individus dont est extrait un échantillon.
- Échantillon : petit nombre de sujets tirés au hasard d’une population. A partir de ses paramètres (m, s) on pourra estimer les paramètres de la population (µ, σ).
Biais n'est pas hasard
Les biais sont des erreurs systématiques liées à la constitution de l’échantillon ou à la mesure (technique, mauvais tarage, appareils différents…) et sont corrigibles, différents donc de l’erreur aléatoire, non corrigible.
Exemple de biais : si on mesure la tension artérielle (TA) avec un sphyngomanomètre ou avec un cathéter intra-artériel on obtiendra des valeurs différentes.
Distributions des variables aléatoires
- Distributions :
- Des variables continues : distributions gaussienne (= normale), logarythmico-normale
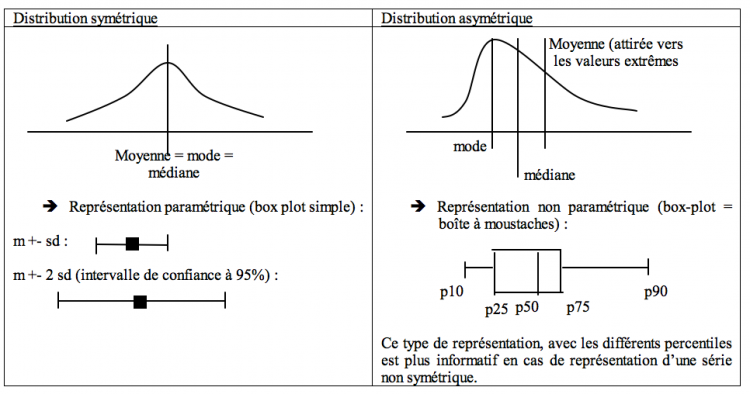
- Distribution gaussienne : on construit une courbe de probabilité basée sur une loi de distribution postulant que l’intervalle de prédiction [m +- s] contient 68% des valeurs et [m +- 2s] contient 95% des valeurs. La surface totale étant de 100% et la médiane = le mode = la moyenne.
- Des variables discrètes : distributions hypergéométriques, binomiales, de Poisson
- Des variables continues : distributions gaussienne (= normale), logarythmico-normale
- Lois de probabilités sur de petits échantillons : tests de student, du chi², de Fisher,… nécessitent un degré de liberté (d.d.l.)
Statistiques descriptives : calcul des paramètres
Les paramètres sont des variables caractérisant une distribution théorique connue, permettant de déterminer la forme exacte de cette distribution. Ils permettent de résumer (réduire) un grand nombre de données. On fait souvent l’hypothèse que dans une population déterminée la variable a une distribution de forme théorique connue. Ex : une distribution gaussienne se caractérise par deux paramètres : moyenne et variance.
Il existe des tests paramétriques (= test statistique dont le calcul est basé sur les paramètres. Supposant un écart-type sd symétrique de part et d’autre de la moyenne m) et non paramétriques (test statistique dont le calcul n’est pas basé sur les paramètres mais sur les rangs pour la comparaison de deux ou plusieurs groupes dont la distribution des valeurs observées n’est pas gaussienne).
Est variable tout ce qui varie dans un exemple de donné. Qualifiée d’aléatoire si les valeurs qu’elle peut prendre fluctuent au hasard.
- Variables qualitatives catégorielles : nominales (ex : fumeur/ non fumeur) ou ordinales (ex : groupes d’âges 10-19/ 20-29/…)
- Variables quantitatives : discrètes (dénombrements. Ex : nombre de décès) ou continues (mesures. Ex : poids)
Paramètres de position et paramètres de dispersion
- Paramètres de tendance centrale (= de position) : moyenne (arithmétique = somme des valeurs/ nombre de valeurs, géométrique, harmonique, quadratique), médiane (= percentile 50 = divisant la population en deux groupes contenant chacun 50% des individus), mode (= valeur la plus fréquente).
- Dans le cas d’une distribution normale (symétrique), moyenne = mode = médiane
- Paramètres de dispersion :
- Ecart-type (s = SD), qu’on ne peut calculer directement (les – neutralisant les +) mais par le biais de la racine carrée de la variance.
- Variance = s² = ( ∑ (Xi – m)² ) / (n-1)
- (n-1) exprimant l’existence d’un degré de liberté d.d.l.=1
- Amplitude (= maximum – minimum), coefficient de dispersion/ de variation (= 100 x sd/m), écart interquartile (= p75 – p25)…
La notion de degré de liberté (d.d.l.) se réfère au nombre de termes linéairement indépendants impliqués dans le calcul d’un paramètre. Il est calculé comme la taille de l’échantillon moins le nombre de paramètres nécessaires pour le calcul de ce paramètre. Ainsi pour une distribution normale : d.d.l. = 0 pour le calcul de la moyenne (on divise par n), d.d.l.=1 pour le calcul de la variance (on divise par n-1).
Symétrie et représentation graphique
Plus la valeur (moyenne – médiane) est éloignée de 0, plus la série est asymétrique.
Indépendance et covariance
Deux variables sont indépendantes lorsqu’il n’existe pas de corrélation entre leurs séries de valeurs (les variations d’une variable Y ne sont pas liées aux variations de la variable X). L’indépendance traduit donc que la connaissance de la réalisation d’un événement ne nous donne aucune information sur la réalisation d’un autre événement. Cette notion est importante car elle déterminera notamment le mode de calcul du test statistique utilisé pour la comparaison de deux moyennes.
Ex : l’âge et la TA sont deux variables non indépendantes : la TA systolique augmente et la TA diastolique diminue avec l’âge (baisse d’élasticité des artères liée à l’âge : se dilatent moins en systole et se contractent moins en diastole).
Comment calculer le degré d’indépendance entre deux variables ? Par le biais de la covariance :
Cov = ( (Xi – m1) x (Yi – m2) ) / (n – 1)… Une covariance = 0 signifie que les deux variables aléatoires sont indépendantes. Cependant, ce paramètre doit encore être transformé pour être facilement interprété : on calcule le Coefficient de corrélation : r = cov / ( √variance1 x √variance2).
Si ce coefficient est proche de ses valeurs extrêmes 1 ou -1, il existe une corrélation directe ou inverse (souvent une relation causale).
Variance de la différence entre deux moyennes
- Si les variables ne sont pas indépendantes :
- Var (mx-my) = 1/n x (varx + vary – 2 covxy)
- Ex : test t = (mx – my) / [√(var (mx – my)] avec d.d.l. = nx + ny – 2
- Var (mx-my) = 1/n x (varx + vary – 2 covxy)
- Si les variables sont indépendantes : idem mais covxy = 0
Estimation de la précision d'une moyenne
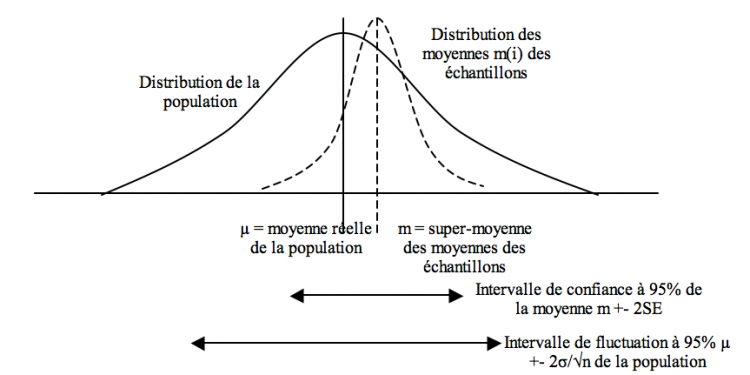
Imaginons une population (µ, σ) dont on tire n échantillons (m(n), sd(n)). On peut alors construire une « superdistribution » avec une « supermoyenne » m (estimant µ) et une « erreur standard » SE = sd/ √n (« super écart-type » estimant SE = σ/√n).
On peut alors bâtir un intervalle de confiance à 95% = m +- 2 SE estimant la précision de la moyenne (la moyenne réelle a 95% de chances de se trouver dans cet intervalle) : 95% de ces intervalles, calculés via les paramètres de chaque échantillon, contiendront la moyenne de la population.
L’intervalle de fluctuation µ +- 2σ/√n de la population : intervalle, calculé via les paramètres de la population, contenant 95% des moyennes échantillons
L’intervalle de prédiction pour un individu m +- 2 sd
En pratique, des études sont compatibles si et seulement si l’intervalle de confiance de la moyenne de l’une contient la moyenne de l’autre. Ainsi :
Intervalles de confiance d'une proportion
On peut raisonner de la même façon pour une proportion, les paramètres étant alors p et SE, estimations de pi et SE.
SE = (√ (p x (1 – p))) / √n
La variance étant p x (1 – p)
Statistiques inférentielles
Formulation d'hypothèses (tests d'hypothèse = test de signification)
Une hypothèse statistique est une assertion concernant la distribution d’une ou plusieurs variables aléatoires.
Les tests statistiques ne nous permettent que de rejeter une hypothèse avec un certain degré de certitude. Si l’on se pose une question (HA), il faut donc tester l’hypothèse alternative (inverse) (Ho) pour voir si l’on peut la rejeter avec un degré de certitude suffisant. Ainsi, si l’on veut démontrer l’existence d’une différence, on part d’une hypothèse nulle Ho (postulant l’absence de différence = les différences observées peuvent être expliquées par le hasard) qu’on va essayer de rejeter par un test statistique… On obtient alors une valeur de p. Si :
- p < 0,05 → ok = significatif = il n’y a que 5% de chances que le hasard suffise à expliquer les différences observées à Ho est rejetée : il y a une différence
- p > 0,05 → ko = non significatif = il y a plus de 5% de chances que le hasard suffise à expliquer les différences observées à on ne peut rien dire (peut-être est-ce un hasard… peut-être pas…).
On distingue les
- études de supériorité : Ho : m1 = m2 → Ho ko (HA ok) si p < 0,05 → m1 est différent de m2 !
- études d’équivalence : Ho : m1 est différent de m2 → Ho ko (HA ok) si p > 0,05 → m1 = m2 !
Tests d’égalité = d’homogénéité (vérifier si l’écart entre les moyennes de deux échantillés peut-être considéré comme fortuit), de conformité (vérifier si un échantillon peut être considéré comme extrait d’une population), d’indépendance (vérifier l’indépendance stochastique de deux ou plus critères de classification), d’ajustement (vérifier si un échantillon suit à tout point de vue une distribution donnée : gaussienne, de Poisson,…).
Erreurs et fluctuations d'échantillonnage
Il est ici question d’intervalles de confiance de la moyenne (pas de l’intervalle de prédiction des individus)
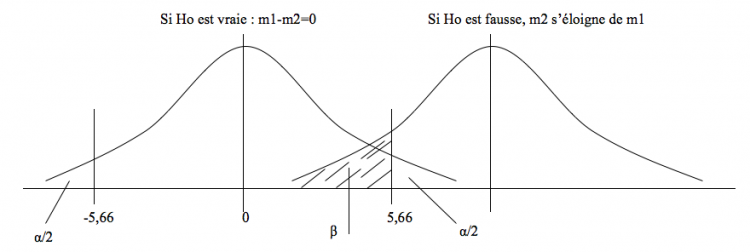
Erreur de type 1: α
Les fluctuations d’échantillonnages sont liées au hasard et peuvent nous conduire à conclure qu’il existe une différence, même en l’absence de différence réelle ! Le fait de choisir p = 0,05 limite cette erreur α à 5%, chiffre arbitrairement choisit comme seuil international de signification.
= rejeter Ho alors qu’elle est vraie (p < 0,05… mais pas de bol on est en plein dans ce 0,05…)
Erreur de type 2 : β
Inversement, ces fluctuations peuvent nous conduire à conclure qu’il n’existe pas de différence, alors qu’il existe une différence réelle ! Cette erreur, elle, n’est pas fixée, mais dépend du nombre de sujets (augmenter n revient à reserrer les distributions) et de l’importance de la différence (l’erreur de type 2 baisse si la différence est plus importante, ce qui peut être obtenu en augmentant par exemple la dose d’un médicament versus placebo). On a arbitrairement choisit une valeur maximale de β = 20% comme acceptable.
= accepter Ho alors qu’elle est fausse
Si Ho est vraie, les 2 courbes se superposent et on a un risque d’erreur α d’avoir un échantillon dont la moyenne se situe en dehors de l’intervalle de confiance (IC) de la moyenne. Si Ho est fausse, les 2 courbes s’éloignent et on a un risque β que m2 se situe dans l’intervalle de confiance de m1…
|
Ho vraie (pas de différence) |
Ho fausse (différence) |
Acceptation (pas de différence) |
Correct |
Erreur β |
Rejet (différence) |
Erreur α |
Correct |
La puissance
Autre façon de quantifier l’erreur de type 2 : puissance = 1 – β. La puissance d’une étude doit donc être supérieure à 80% pour être considérée comme suffisante, ce qui signifie qu’il y 80% de chances de mettre en évidence une différence significative si elle existe.
Certains calculs permettent de déterminer une taille n de l’échantillon ou une dose nécessaire pour obtenir une puissance suffisante.
p renseigne sur l’importance du hasard dans les résultats (ex : il existe une différence entre les groupes placebo et médiqué), mais pas sur l’importance de ces résultats (ex : forte ou faible différence). Il peut exister une différence significative mais sans/peu d’importance clinique. Inversement, une différence non significative peut avoir une importance clinique.
En cas de résultat non significatif, il est très important de s’intéresser à la puissance.
Les tests statistiques
Comparaison de deux moyennes : tests de Student (t)
La première chose à faire est de savoir si l’on a affaire à des échantillons indépendants ou pairés (design expérimental)
Echantillons indépendants
Comparer les variances
Via le test de F (= s(1)²/s(2)²) avec ddl 1 et 2 = n-1
Si on obtient un p correct (>0,05 : on ne peut rejeter l’égalité des variances) on conclut que les variances sont comparables et on les remplace par une variance moyenne (ou variance poolée) s (= (ddl1 x s1 + ddl2 x s2) / n1+n2 -2
Si les variances ne sont pas comparables, des formules supercompliquées et dépassant le cadre de cet article permettent de s’en sortir.
Comparer les moyennes en cas de variances « égales »
On utilise le test de student t = [m1 – m2] / (s x √ (1/n1 + 1/n2) ) avec ddl = n1 + n2 – 2
On obtient un p, significatif ?
Exemple :
Etude sur l’HTA avec 2 groupes de 5 placebos (m = 174,4 ; sd = 4,93) et 5 béta-bloquants (m = 168 ; sd = 3,94)
- Comparer les variances : F = 1,57 avec ddl1 et ddl2 = 4 → p = 0,337 → ok → s = 4,46
- Comparer les moyennes : t = 2,27 avec ddl = 8 → p= 0,053 → p > 0,05 (non significatif) → Ho (m1 = m2) ne peut pas être rejetée et on ne peut rien conclure !
- on pourrait tenter d’obtenir un p significatif en augmentant les n ou/ et en augmentant les doses.
Echantillons pairés
Lorsqu’on utilise des groupes de données non indépendantes, on doit utiliser la covariance. On va en fait calculer les différences entre les deux groupes pour l’éliminer (on élimine ce qui est commun), et calculer la moyenne et le sd des différences.
On utilise alors le test suivant de student t = m(diff) / √ (s²/n) avec ddl = n-1
Exemple :
- Etude sur l’hypertension artérielle (HTA) avec un seul groupe de 5 patients. On mesure leur TA avant (G1) et après (G2) l’administration de beta-bloquants.
- → t = 3,66 avec ddl = 4 à p = 0,0216 à on peut rejeter Ho : la différence est signficative (p < 0,05)
Comparaison de deux proportions : tests de z
Proportions indépendantes
Soit p1 et p2
→ on calcule une proportion moyenne pondérée p = (n1 x p1 + n2 x p2) / n1+n2
→ on utilise le test de z = [p1 – p2] / √( p x (1 – p) x (1/n1+1/n2))
Ex : 2 sondages donnant 38% (n=1000) et 42% (n=500) d’opinions positives → p = 0,393 → z = 1,495 → p = 0,135 → il n’existe pas de différence significative entre ces deux sondages.
Echantillons pairés
On utilise z = [p1 – p2] / √[p1-p2]
Ex : comparaison des effets de la caféine et d’un placebo sur le sommeil. Tous les sujets essaient les 2.
- → Caféine : 8 endormissements difficiles, 23 non. Placebo : 1 difficile (alors qu’il avait facile avec la caféine), 30 non.
- → z = 2,33 à p = 0,019 à on rejette Ho à il existe une différence significative entre le placebo et la caféine.
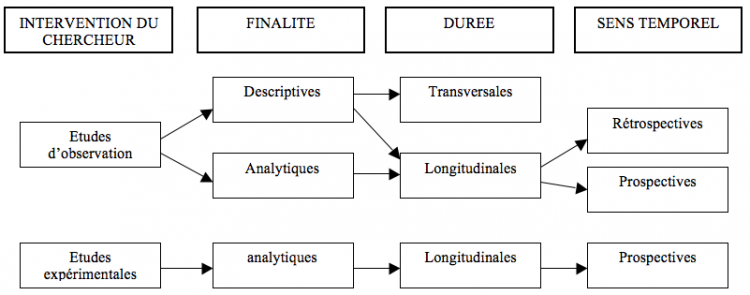
Les études observationnelles
Peuvent être classées selon : finalité/ interventions du chercheur/ calendrier (sens temporel)/ durée
Les types d'études observationnelles
Etudes de cohorte = études prospectives
Désavantages : pas de randomisation, nombreux facteurs confondants, 1 seule question peut être posée, coût, difficile pour les pathologies rares, possibles perte de suivi ou changement de comportement, études parfoois fort longue (si temps de latence élevé)
Avantages : calcul de risque, information sur l'incidence, pas d’ambiguité temporelle, étude de la relation dose-effet
→ principale information : taux d’incidence de la maladie
Design : identifier les patients sains à risque (FR), constituer 2 (ou plus) groupes avec ou sans FR, mesure de l’apparition de la maladie, taux de survenue comparé en fonction de l’exposition.
Etudes cas-témoins = études rétrospectives
Groupe de malade et groupe contrôle → qui a été exposé aux FR ?
Avantages : permet l’évaluation de causes multiples, adapté pour les pathologies rares ou avec période de latence élevée, rapide, moins cher, bonne collaboration du patient (nécessite rarement plus d’1 ou 2 interviews).
Désavantages : données anamnestiques ou sur dossier souvent incomplètes, contrôle des facteurs externes difficile, appariement pas toujours adéquat.
Rétrospectif → biais : absence de double aveugle, biais de détection, biais de sélection, biais liés aux différences de traitement (= facteurs déséquilibrant un groupe en faveur de l’autre).
Design : choisir les cas (malades), établir des contrôles témoins (quelques uns par cas), évaluer chaque groupe à la recherche d’antécédents d’exposition au FR, établir une association entre l’exposition au FR et l’apparition de la malaadie.
Etudes transversales = études de prévalence
De durée brève : à un moment donné/ sur un événement donné tel que l’embauche, l’entrée à l’école.
→ Récolte de données pour ce moment sur l’exposition et la maladie à prévalences de la maladie chez les exposés et chez les non exposés.
Analyse des résultats : tableau de contingence et test du chi2
Tableau de contingence :
|
Variable 2 positive (svt malade) |
Variable 2 négative (svt sain) |
Total |
Variable 1 positive (svt exposition au FR) |
a |
b |
Total marginal N1 |
Variable 2 négative (svt non exposition au FR) |
c |
d |
Total marginal N0 |
Total |
Total marginal M1 |
Total marginal M0 |
Grand total |
→ calculer les proportions : pour une étude prospective : p1 = a/ (a+b) et p2 = c/ (c+d) → p1 est-il différent de p2 ? → Ho : p1 = p2
On pourrait faire un test de z, cependant celui-ci ne permet que de comparer deux proportions 2 à 2. De plus pour un test de z, le design est important : il faut savoir si on est dans le cas d’une étude prospective, transversale (on doit alors utiliser le grand total comme dénominateur pour les proportions) ou rétrospective (on doit alors utiliser comme dénominateurs (a+c) et (b+d) pour les proportions). Le fait qu’on utilise des dénominateurs différents est dû au fait que le design nous impose des totaux fixés différents
Autre alternative = test du chi². Ses avantages sont :
- Peut s’appliquer quelque soit le nombre de proportions (tableaux à x lignes et y colonnes)
- Il se calcule de la même façon quelque soit le design de l’étude → si on ne connaît pas le design, pas de panique : on peut toujours faire un chi²…
Principe du chi² = calculer "ce que le hasard aurait mis comme proportions". Test du chi² = calculer la relation entre le chiffre attendu (celui que le hasard aurait mis) et celui observé. Pour obtenir les chiffres que le hasard aurait distribué, il suffit de prendre p = M1/Grand total et d’appliquer cette proportion à N1 et N0 pour obtenir a et c attendus.
Chi² = ∑ (observé – attendu)²/ attendu avec un ddl = (rangées – 1) x (colonnes – 1)
(chi² = 0 si les nombres observés sont égaux à ceux attendus = différence non significative avec p = 1)
Exemple d’étude prospective : apparition d’une maladie en fonction de la présence d’un FR.
Exemple d’étude transversale : existe-t-il une relation entre bactériurie et HTA chez la femme par l’étude d’un échantillon de la population féminine à un moment donné ?
Exemple d’étude rétrospective : étude du rapport entre alcoolisme et cancer de l’œsophage par étude de dossiers/ anamnèses de cas et témoins.
Evaluation de l'importance de l'effet
Le test du chi² nous permet donc d’établir s’il existe des différences significatives… mais ne nous renseigne pas sur l’importance de ces différences. Pour cela il faut utiliser d’autres outils.
La différence de risque (entre le FR et le risque de base) = DR = risque attribuable (RA) pour les exposés
DR = p1 – p2
Le dénominateur des p varie selon le design de l’étude, de la même façon que pour le test de z. En outre, la DR ne peut être calculée pour les études rétrospectives (car c’est nous qui choisissons le rapport malades/témoins)
Le risque relatif = le rapport de risque = RR
RR = p1/ p2
Le dénominateur des p varie selon le design de l’étude, de la même façon que pour le test de z. En outre, le RR ne peut être calculée pour les études rétrospectives (car c’est nous qui choisissons le rapport malades/témoins)
Ce qui signifie qu’on à RR x plus de chances de tomber malade si l’on présente le FR.
Le rapport des cotes = le Odds Ratio = le rapport des chances contraires = OR
A la différence des DR et RR, le OR peut être calculé pour les études rétrospectives (car les différences se simplifient en cours de calcul). Dans le cas d’une étude prospective on parle de OR de maladie, pour une étude rétrospective de OR d’exposition (au FR) : la signification diffère, mais le calcul est le même.
C’est le rapport des quotes qu’un événement (ex : maladie) arrivant à un groupe arrive à un autre.
Si q1 = 1 – p1 et q2 = 1 – p2 : OR = probabilité de gagner / probabilité de perdre = (p1/q1) / (p2/q2)
Après simplification : OR = a x d / b x c = rapport des produits croisés.
NB : quotes et probabilités :
Selon les cas on peut calculer une « quote en faveur » ou une « quote contre ».
Ex : On veut obtenir un 4 en jetant un dé → p = 1/6 et q = 5/6 → odds en faveur de l’événement = (1/6) / (5/6) = 0,2 (on perdra 5 fois pour chaque victoire)
Ex : On parie sur un cheval qui a 1/6 chances de gagner → odds contre l’événement = (5/6) / (1/6) = 5 → quote de 5 contre 1 (on perdra 5 fois pour chaque victoire)
Intervalles de confiance des DR, RR et OR
Un intervalle de confiance peut être calculé autour de chacune de ces données.
DR
Si DR +- 1,96 SE contient le neutre (ici 0) à cela signifie que le p est non significatif
NB : une DR < 0 signifie qu’il s’agit d’un facteur protecteur, > 0 qu’il s’agit d’un FR
RR et OR
Si RR/ OR +- 1,96 contient le neutre (ici 1) à cela signifie que le p est non significatif.
NB : un RR/ OR < 1 signifie qu’il s’agit d’un facteur protecteur, > 1 qu’il s’agit d’un FR
Réduction relative du risque = RRR = fraction étiologique du risque pour les exposés
RRR = % de malades attribuable au FR chez les exposés = part des maladies que l’on pourrait éviter dans la population à risque en cas d’élimination du FR.
RRR = Risque Attribuable pour les exposés / Risque absolu pour les exposés = [ (a/N1) – (c/N0) ] / (a/N1) = (p1 – p2) / p1
Le number needed to treat = NNT
Représente le nombre de patients à traiter pour avoir un effet bénéfique chez 1 patient.
Interprétation des résultats
Se méfier de la RRR (souvent présenté par les études des firmes !) car elle amplifie fortement les répercussions réelles.
Préférer :
- La DR : très significatif si elle est haute
- Le NNT : très significatif s’il est faible. C’est le chiffre le plus important en pratique car il représente concrètement ce que l’on recherche : un NNT = 5 signifie qu’on aura un effet bénéfique tous les 5 patients en adoptant le traitement proposé.
- Si < 10 à considéré comme effet significativement positif
- Si entre 10 et 100 → zone floue, difficilement interprétable
- Si > 100 → on considère que le traitement proposé ou l’élimination du FR n’aura pas d’effet visible
Avoir établit une association (résultat significatif) n’équivaut pas à établir un lien de causalité ! Pour cela la randomisation est un argument puissant. Cependant, même en l’absence de randomisation (études cas-témoins par exemple) on peut se baser sur 5 critères pour établir un lien de causalité :
- Reproductibilité des résultats
- Intensité de la relation (RR important)
- Spécificité (moins il y a de FR impliqué, plus le rôle causal du FR étudié est vraisemblable)
- Relation temporelle : la cause précède l’effet !
- Plausibilité (biologique, physiopathologique, pharmacologique,…)
Incidence et prévalence
Prévalence = nombre de malades par rapport à la population à un moment donné. = n malades/ x hab < études transversales
Incidence = nombre de nouveaux malades chaque année dans une population donnée = n cas / x hab / an < études prospectives
Ces deux concepts apportent des infos très différentes. Ex : l’efficacité du traitement contre le SIDA n’a pas changé son incidence (reste ~) mais bien sa prévalence (augmentée puisque les malades survivent bien plus longtemps).
Densité d’incidence : utilise comme dénominateur la durée d’exposition au risque = nombre de nouveaux cas/ x jours-patients
Taux de mortalité
= nombre de décès par an rapporté à une population donnée en milieu de cette année.
Des taux de mortalités identiques peuvent avoir des significations très différentes selon la population. Ex : le taux moyen de décès est sensiblement le même (~12%) en Belgique (population vieille) et au Maroc (population jeune)… alors que le taux de mortalités par tranche d’âge sont nettement plus élevés au Maroc qu’en Belgique quel que soit l’âge… mais en Belgique la tranche d’âge des > 50 ans est sur-représentée.
→ Utilisation de :
- Taux de mortalité spécifique par tranche d’âge
- Taux standardisés : le SMR (standardized mortality ratio) présente ce que serait la mortalité si la population présentait une structure de tranches d’âges "standard" (généralement celle du monde ou de l’Europe). Il permet des comparaisons entre régions présentant des vieillissements différents et constitue le gold standard en matière d’évaluation hospitalière. "calculé comme le rapport du nombre de décès observé sur le nombre de décès attendus calculé par méthode indirecte"
Taux de létalité
= nombre de décès attribuables à une maladie durant une période donnée / nombre de cas de cette maladie sur cette période = potentiel létal d’une maladie.
Taux de mortalité proportionnel
= nombre de décès attribuables à une maladie durant une période donnée/ nombre total de décès dans la population durant la même année. = part de la mortalité totale attribuable à une cause donnée.
Tableaux de survie démogrpahique et espérance de vie
Un tableau de survie est calculé en partant du taux de mortalité spécifique pour l’âge. On calcule ensuite ce qui arriverait à la cohorte depuis la naissance si les taux de mortalité spécifiques pour l’âge s’appliquaient sans modification sur une vie entière.
L’espérance de vie à un âge donné = durée de vie moyenne pour les sujets ayant cet âge.
Essais comparatifs = essais cliniques = études expérimentales
Effet observé = effet réel + erreur aléatoire (varie selon la puissance) + erreur systématique (biais = erreurs systématiques généralement involontaire, plus ou moins difficile à déceler, qui fausse la comparaison de deux groupes, l’évaluation d’un critère diagnostique, etc…)
Phases cliniques du développement d'un médicament
Phases cliniques de développement d’un nouveau médicament :
- phase 1 : détermination de l’innocuité, c'est-à-dire de la dose maximale tolérable. On utilisera alors en clinique la dose = dose(max) / 2
- phase 2 : étude des effets (thérapeutiques et ES) pour l’administration de la dose déterminée en phase 1
- phase 3 : comparaison des effets du médicaments vs un placebo ou un autre médoc.
- phase 4 : après la mise sur le marché, évaluation des Es (pharmacovigilance), autres utilités,…
On va s’intéresser ici aux essais de phase 3.
Méthodes d'échantillonage et randomisation
Il ne faut pas confondre comparabilité (randomisation) et représentativité (technique d’échantillonnage).
Randomisation = tirage au sort d’individus parmi un groupe pour établir des sous-groupes comparables. Elle élimine les sources de biais (sauf biais accidentel [déséquilibre entre traitements lié au hasard seul]). Elle valide les tests statistiques utilisés pour comparer les traitements.
La représentativité
La représentativité d’un échantillon s’améliore lorsque chaque personne de la population à une chance égale d’être tirée au sort (échantillon aléatoire simple = méthode probabiliste).
Cependant ce n’est pas toujours le cas. Pour améliorer la représentativité de son échantillon, on peut alors utiliser des quotas (après avoir étudié la structure de la population). Un exemple type est la constitution d’un échantillon sur base du volontariat. On s’éloigne encore plus de la population de base si l’on recrute parmi les patient de l’hopital. Etc.
Le tirage au sort
A l’aide d’un générateur de nombres aléatoires, parmi une base de donnée (ex : tirage au sort de 40 personnes parmi 1000, pour constituer deux groupes de 20 patients) à distribution de x patients dans les différents groupes.
La randomisation minimise les biais de sélection (équilibre entre les groupes, aussi bien pour les facteurs connus qu’inconnus [facteurs inconnus = facteurs confondants]).
La modélisation est différente : il s’agit d’un algorythme permettant d’équilibrer/ d’ajuster les facteurs connus.
NB :
- dans le cas d’une population bien définie (dont on connait la réponse au traitement classique = dont on connaît les paramètres) et d’un échantillon aléatoire possible à besoin d’un seul échantillon aléatoire simple recevant le nouveau traitement à comparaison à la population
- dans le cas d’une population mal définie et d’un échantillon aléatoire possible à constitution de deux groupes aléatoires simples à comparaison des deux groupes à généralisation à la population
- dans le cas d’une population mal définie et d’un échantillon non aléatoire (non représentatif de la population, ex : patients de l’hopital) à constitution de deux groupes non aléatoires par randomisation à généralisation uniquement à la population concernée (ex : patients hospitalisés).
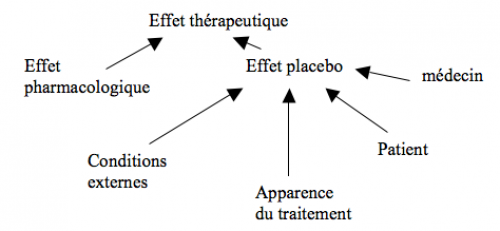
Le placebo
Placebo = médicament factice ne contenant aucune substance active. Effet placebo = placebo entraînant des effets positifs (amélioration de la maladie non attribuable au hasard ou à l’évolution naturelle de la maladie = effet bénéfique non spécifique)
Effet nocebo = idem mais entraînant des effets négatifs (ES)
Au sens large, l’effet placebo dépend de :
- facteurs spécifiques à la maladie :
- les effets placebo jouent moins dans les maladies chroniques
- facteurs non spécifiques (sensibilité variable selon les patients, importance variable selon l’attitude des médecins, l’environnement,…) :
- effet blouse blanche
- effet Hawthorne (le simple fait que le patient participe à une étude et que l’on s’intéresse à lui accroit sa motivation et peut influencer son état)
- auto-suggestion liée aux croyances et attentes du patient
- hétérosuggestion liée aux croyances et attentes des médecins
- lié à l’apparence et autres caractéristiques du traitement
- lié à l’environnement de l’expérience
L’évaluation de son impact est très important dans les études cliniques car, si un tt A marche mal mais que l’effet placebo y est très important on conclura à un résultat positif similaire à celui d’un tt B marchant très bien mais où l’effet placebo n’a pas joué à si on veut pouvoir les comparer, il faudra établir des groupes placebo pour A et pour B.
L’évaluation médicale finale de l’étude dépend de :
Statut initial du patient + histoire naturelle de la maladie + effet thérapeutique du traitement+ erreurs de mesures
Exemples de l’impact de l’administration d’un placebo : parkinsonisme (6-18% d’amélioration subjective), angoisse (30% d’amélioration), ulcère GD (55-88% d’amélioration), douleur (40% d’amélioration [ !!!versus « seulement » 60% pour la morphine !!!])
Puissance de l'essai clinique
= capacité à détecter une différence entre deux traitements lorsque cette différence existe. P = 1 – erreur β. P doit être supérieure à 80%, elle augmente en fonction du nombre de sujet et de la dose administrée.
Les biais de l'essai clinique
Biais de sélection
= on a constitué un groupe dont un facteur risque d’influencer la réponse au traitement par rapport à l’autre groupe. Eliminés par la randomisation.
Biais de susceptibilité
= on a constitué un groupe dont l’état de base risque d’influencer la réponse au traitement par rapport à l’autre groupe. Eliminés par la randomisation.
Biais de procédure (= de performance)
= l’exposition au traitement n’est pas identique. Ex : administration per os dans un groupe et IV dans l’autre (effet subjectif différent, compliance différente,…)
Biais de détection (= d'outcome)
= évaluation différente des résultats selon les groupes. Peut être éliminé par la pratique du « double aveugle »
Biais de transfert
= perte de patients durant l’étude (certains ne viennent plus, ont a du exclure d’autres, on a du stopper pour certains du fait d’ES,…) à formation d’un déséquilibre entre les deux groupes.
Ils ne peuvent être corrigés mais on peut en tenir compte dans l’analyse des résultats :
- analyse per protocole = exclusion de patients sur base d’infos obtenue après randomisation à étude l’efficacité pharmacologique… le problème c’est que lorsqu’on retire des patients de groupes randomisés, on perd l’effet randomisation…
- analyse en intention de traiter = évaluation globale de l’efficacité du traitement : on considère que les « biais de transfert » seraient également présent dans la réalité… et que dans ce cas on n’évalue pas seulement l’effet intrinsèque du traitement mais également la compliance qu’il entraîne, sa facilité d’administration,… C’est la méthode qui semble la meilleure.
- ainsi, si une infirmière commet une erreur dans l’administration traitement d’un patient du groupe A, on garde néanmoins le patient dans ce groupe. De même, si un patient du groupe A meurt fortuitement durant l’étude, on le garde dans les résultats.
Validité
On peut distinguer :
- la validité interne d’une étude, qui est maximale si l’étude répond à :
- la randomisation
- un groupe contrôle
- procédure en double aveugle
- la validité externe : peut-on généraliser les résultats à la population ? Cela dépend :
- des critères d’inclusions : plus ils sont larges, plus la généralisation prend sens
- de la représentativité de l’échantillon… en pratique l’extrapolation est rarement possible.
Méta-analyses sur les essais randomisés
La présentation par diagramme de Forest nous apporte de nombreuses informations :
- si l’intervalle de confiance de l’OR contient 1 à non significatif
- un intervalle de confiance trop grand signifie généralement que le nombre de sujets n’est pas suffisant. En l’augmentant, on peut diminuer l’IC et, éventuellement en exclure 1…
Test d'hétérogénéité
On fait un test de chi² pour savoir si on peut rejeter Ho (études homogènes). S’il est significatif cela signifie que les résultats d’au moins une des études n’est pas compatibles avec les autres. S’il n’est pas significatif, Ho ne peut être rejetée, et on considérera que l’homogénéité est suffisante pour faire l’analyse.
La variance de chaque étude
Sur le diagramme de Forest, la variance correspond à la boîte sans ses moustaches (plus elle est grande, plus la variance interne de l’étude est grande).
L'EBM : Evidence Based Médicine
= pratique clinique basée sur les niveaux de preuve des études motivant cette pratique.
Comparaisons multiples et dérives de l'erreur α
Imaginons que nous voulons comparer n échantillons (1 contrôle et 2 traitements p ex)… peut-on envisager de comparer les échantillons 2 à 2 par des tests t et de rejeter l’hypothèse d’égalité si au moins un des tests la rejette pour un couple d’échantillon ? Non ! Pourquoi ? Du fait de l’erreur α : imaginons que les distributions dont sont issus les échantillons soient effectivement identiques (équivaut à une distribution commune) à on s’attend à ce que les moyennes des échantillons soient proches de la moyenne de la « distribution commune »… cependant plus on tire d’échantillons, plus on prend le risque d’en prendre un dans les extrêmes définis comme non significatifs… et de rejeter à tort l’hypothèse d’égalité… c’est l’inflation de l’erreur α.
En fait, si on prend p = 0,05 pour une étude (une comparaison), on a pour n comparaisons p = n x 0,05 x 0,95^n
Ainsi si une telle méthode était appliquée à 3 échantillons (3 comparaisons), l’erreur résultante serait de 13%... et de 23% pour 4 traitements (6 comparaisons)… ce qui ne peut être acceptable !
Comment résoudre le problèmes ?
On fait d’abord une analyse de variance (ANOVA) qui permet de dire si une moyenne au moins diffère significativement des autres (mais on ne sait ni laquelle, ni combien) à on obtient une valeur de F. Si elle est < 1, on ne rejette pas Ho (moyennes identiques). Si elle est > 1, il faut alors recourir à une méthode de correction complexe. Diverses méthodes de correction existent : corrections de Bonferroni, de Sidak, de Tukey, test de student modifié,…
Designs expérimentaux
Essais en parallèles
= étude classique, 2 groupes différents dont on compare les moyennes
Essais croisés = cross over
Dans ce type d’étude, chaque sujet est son propre témoin. à nécessite 2 périodes d’expérimentation (administration séquentielle de deux traitement).
Les avantages :
- diminution de la variance résiduelle (élimination de la variabilité inter-individuelle)
- nécessite moitié moins de sujets à économies et pratique pour les maladies rares
Les désavantages :
- ne peut s’appliquer à tous les traitements (ex : si le patient est guéri à la première étape, la seconde est impossible) et il faut que la maladie n’évolue pas entre les traitements.
- Effet carry-over : le traitement A n’aurait-il pas continué à agir durant le traitement B, ou du moins modifié son activité ?
→ Evaluation statistique difficile nécessitant des outils particuliers.
Designs factoriels
= cas particulier de stratification. Consiste incluant au moins deux facteurs. x^y
Ex : design factoriel 2² : double randomisation sur des patients atteints d’un cancer rectal :
- Randomisation 1 à 2 groupes : radiothérapie et pas de RXth
- Randomisation 2 de chacun de ces deux groupes à Chimiothérapie et contrôle
- → au final : 4 groupes : contrôle, RXth, Chth, RXth + Chth
Estimation de l’effet des traitements a et b pour un 2² avec 4 groupes X Xb Xa et Xab :
- Effet du traitement A = ½ x [ (Xa-X) + (Xab-Xb) ]
- Interaction AxB = [ (Xab-Xb) – (Xa-X) ] = [ (Xab-Xa) – (Xb-X) ]
Avantages :
- Plus efficient qu’un design en parallèle car il permet d’obtenir une précision équivalente avec moins de mesures (donc de sujets) : pour un 2², 4 mesures permettent d’obtenir la même précision qu’avec 6 en parallèle. Il nécessite cependant plus de sujets qu’un crossing-over. Si un design parallèle nécessite (pour une puissance identique) 1 sujet, le cross-over (2x2) en nécessite 0,5 et le design factoriel (2²) 0,66667
- Permet d’estimer les interactions entre plusieurs médocs (effet synergique ou antagoniste) ou l’absence d’interaction (simple effet additif).
- Peut-être utilisé pour des tts qui n’ont rien à voir, dans le seul but de diminuer le nombre de sujets (on traite alors les données séparément et on publie 2 études)
L'analyse séquentielle
Dans un essai séquentiel, le nombre de sujets n’est pas calculé au préalable : l’essai est analysé de manière répétée (tous les x patients inclus) au fur et à mesure de l’obtention des résultats et l’on recrute les patients paquets par paquets. Chaque analyse intermédiaire porte sur l’ensemble des sujets inclus depuis le début de l’essai, et 2 statistiques sont calculées : la différence entre les traitements (Z) et la quantité d’infos accumulées (V), ce qui permet d’obtenir un point pour chaque analyse. Le design séquentiel est délimité par des frontières, calculées par un test triangulaire uni- ou bilatéral et dépendent des taux d’erreurs α et β, de la différence à mettre en évidence, de la fréquence des analyses intermédiaires prévues. Lorsque le trajet reliant les points franchit une frontière, l’essai est arrêté et la conclusion obtenue.
Ce type d’essai permet généralement de réduire le nombre de sujets nécessaires.
Pose cependant des problèmes : si le recrutement (période d’inclusion) dure 2 ans et que le tt a un effet déjà 2 mois après le début, peut-on garder les autres sous placebo (éthique) ? De plus, lorsque les périodes d’inclusion sont très longues, le mode de vie des sujets est susceptible de se modifier. Si lors des analyses intermédiaires, Z est trop petit, on doit arrêter (augmentation de n !!!). Idem pour un Z très grand (d’évidence très efficace ou trop toxique).
En outre, si on multiplie les analyses intermédiaire, on assiste à une dérive de l’erreur α à on doit imposer des p très faibles aux premières analyses intermédiaires pour pouvoir obtenir un p < 0,05 au final.
Les essais d'équivalence
Lorsque dans un essai classique, la supériorité n’est pas significative, il peut être tentant de conclure à une équivalence… mais :
- La puissance peut-être insuffisante
- Conclure ainsi revient à changer d’hypothèse (on testait une hypothèse de différence)
- Les contraintes d’un essai d’équivalence sont différentes de celles d’un essai de supériorité
Les essais d’équivalence ne concluent pas à une efficacité identique par rapport au tt de référence mais à une efficacité suffisante (pas de différence importante d’un point de vue clinique).
Il s’agit de tests unilatéraux (Ho : (m1 – m2) < -delta à p < 0,025 indique une équivalence significative.
Pour démontrer l’équivalence, il faut :
- Que l’IC à 95% centré sur la différence observée soit compris entre –delta et +delta
- Que l’IC à 95% centré sur la différence observée ne contienne pas 0
La décision médicale
Le théorème de Bayes (théorème de l’inversion des probabilités conditionnelles) et les valeurs prédictives
Notion importante : chance à priori (prévalence) et chance à posteriori (VPP) après un premier test. Ex : patient fumeur 51 ans avec douleur thoracique → chance à priori d’un infarctus = 0,5 → enzymes et ECG + → chance à posteriori > 0,9. Mais si patient sportif de 19 ans avec douleur thoracique → chance à priori < 0,2 → enzymes et ECG + → chance à posteriori > 0,4. La démarche clinique doit consister à faire augmenter la chance à posteriori.
Le théorème de Bayes permet de calculer la probabilité des causes à posteriori (maladies si présence d’un signe/ symptôme = VPP) à partir de la connaissance de :
- La probabilité de l’effet (symptômes, signes) lorsque la cause (maladie) est présente (= la sensibilité du signe, dans chacune des maladies comportant ce signe).
- La probabilité à priori des causes (prévalences des maladies présentant ce signe).
Pr (M1/S) = Pr (S/M1) x Pr (M1) / ∑de i=1 à k [ Pr (S/Mi) x Pr (Mi) ]
Ex concret : homme de 60 ans non fumeur avec une toux chronique. La biopsie pulmonaire est compatible avec un cancer bronchique ou une sarcoïdose. On a :
- P (toux / bonne santé) = 0,001
- P (toux/ néoplasie) = 0,9
- P (toux/ sarcoïdose) = 0,9
- P (bonne santé) = 0,99
- P (néoplasie) = 0,001
- P (sarcoïdose) = 0,009
→ On peut calculer les différentes probabilités à posteriori :
- P (bonne santé / toux) = 0,001 x 0,99 / (0,001 x 0,99 + 0,9 x 0,001 + 0,9 x 0,009) = 0,099 = 10%
- P (néoplasie / toux) = 0,09 = 10%
- P (sarcoïdose/ toux) = 0,811 = 80%
Même cas mais fumeur (prévalences différentes) → BS : 5%, néo : 71%, sarcoïdose : 24%
! En dehors des cas où les sensibilités et spécificités des tests = 100%, la VPP diminue très vite avec la diminution de la prévalence. Un test négatif avec une prévalence très basse à grande chance d’un vrai négatif (VPN très élevé). Un test positif avec une prévalence très élevée à grande chance d’un vrai positif.
Les sensibilités et spécificités sont donc des propriétés intrinsèques d’un test. Les propriétés extrinsèques étant :
- Statiques : VPP et VPN
- Dynamiques : rapports de vraisemblance d’un test positif et d’un test négatif.
VPN et VPP
- La VPP = valeur prédictive positive = probabilité que le patient soit malade si le test est positif
- VPP = VP / (VP + FP)
- La VPN = valeur prédictive négative = probabilité que le patient ne soit pas malade si le test est négatif
- VPN = VN / (VN + FN)
Les rapports de vraisemblance : Likehood Ratio
Autre moyen de résumer la sensibilité et la spécificité. Alternative à la courbe ROC (cf épidémiologie).
On définit :
- Le LR positif = VP / FP = (sensibilité) / (1- spécificité)
- = proportion entre la probabilité d’avoir un test positif chez un malade et la probabilité d’avoir un test positif chez un non malade
- Le LR négatif = FN / VN = (1 – sensibilité) / (spécificité)
- = proportion entre la probabilité d’avoir un test négatif chez un malade et la probabilité d’avoir un test négatif chez un non malade
Ces rapports de vraisemblance sont également indépendants de la prévalence et permettront de calculer les VPP et VPN.
Ils offrent une aide précieuse à la décision diagnostique. Ex : un test avec un LR+ = 2,3 à signifie que si le test est positif, il est 2,3 x plus probable que le patient soit malade plutôt qu’il ne le soit pas. Ex : un test avec un LR- = 0,2 à signifie que si le test est négatif, il est 0,2 x plus probable que le patient soit malade plutôt qu’il ne le soit pas (autrement dit : il est 5 x plus probable que le patient ne soit pas malade plutôt qu’il ne le soit).
Valeurs seuil et choix d'un test diagnostic
Il n'y a pas de choix univoque, chaque cas clinique étant particulier. De manière générale, on peut dégager quatre postulats relatifs au choix pratique des tests (Galen et Gambino) :
- Un test sensible est à préférer si :
- Maladie grave et accessible à un traitement potentiellement efficace
- Lorsque le fait de savoir qu’on n’a pas la maladie a une importance sanitaire
- Lorsque les résultats faussement positifs n’ont pas de conséquences économiques ou psychologiques pour le patient
- Ex : phénylcétonurie, tuberculose,...
- Un test spécifique est à préférer si :
- Maladie non ou difficilement curable
- Lorsque les résultats faussement positifs peuvent être économiquement ou psychologiquement traumatisants
- Ex : sclérose en plaques, cancer broncho-pulmonaire,...
- Un test avec une VPP très élevée est à préférer si le traitement des patients a des conséquences graves et irréversibles
- Ex : lobectomie pour suspicion de cancer pulmonaire
- Un test optimal (PCC maximal) doit être préféré
- Lorsque la maladie est grave mais curable
- Lorsque les résultats faussement positifs et faussement négatifs sont tous deux traumatisants et ont des conséquences graves
- Ex : diabète de type I, infarctus myocardique.
Une forte sensibilité (peu de FN) est souhaitable lorsque l’on veut exclure la maladie, une forte spécificité (peu de FP) est souhaitable lorsque l’on veut confirmer une maladie.
Régression vers la moyenne = répétition des tests
Lorsqu’une maladie est rare, on se méfie des tests positifs. Lorsqu’une maladie est fréquente, on se méfie des tests négatifs → intérêt de recontrôler.
Stratégie en série
Soit deux tests t1 et t2. Soit T l'interprétation des deux tests. Deux tests t1 et t2 sont dit mis en série si l'interprétation T est jugée positive lorsque t1 et t2 sont positifs et négative lorsque t1 ou t2 est négatif. Elle implique une perte de sensibilité. Surtout intéréressant pour affirmer raisonnablement la présence d'un trouble rare (contrôle des tests positifs).
Ex : Populations à faible prévalence → faible VPP → on répète plusieurs fois le même test sur les sujets détectés + → amélioration de la VPP. Test avec sensibilité de 90% sur prévalence de 10% à VPP = 50% ! Aucun intérêt pratique ! Mais si on le répète sur les sujets + → VPP = 90%. Si on le répète encore → VPP = 98,78% !
Stratégie en parallèle
Soit deux tests t1 et t2. Soit T l'interprétation des deux tests. Deux tests t1 et t2 sont dit mis en parallèle si l'interprétation T est jugée positive lorsque t1 ou t2 est positif et négative lorsque t1 et t2 sont négatifs. Elle n'implique pas de perte de sensibilité. Surtout intéréressant pour affirmer raisonnablement l'absence d'un trouble fréquent (contrôle des tests négatifs).
Ex : Populations → haute prévalence à faible VPN → on répète plusieurs fois le même test sur les sujets détectés - → amélioration de la VPN. Test avec sensibilité de 90% pour une prévalence de 90% → VPN = 50% → on refait encore le test 2x → VPN = 98,9% !
Combinaison de plusieurs tests en série
En cas de faible prévalence, appliquer le plus sensible en premier → minimise les faux positifs de T, maximise la VPP
Ex : HIV (prévalence = 0,03%)? Test Elisa (sensibilité = 97%) → VPP = 12,7% + Western Blot (sensibilité = 95%) → VPP = 99,93%
Combinaison de plusieurs tests en parallèle
En cas de haute prévalence, appliquer le plus sensible en premier → minimise les faux négatifs de T, maximise la VPN
Ex : toxicomane HIV (prévalence = 60%) ? Test Elisa → VPN = 95,68% + Western Blot → VPN = 99,77%
Courbes ROC (Reveiver Operating Curve) : choix d'un seuil (et donc d'une sensibilité et d'une spécificité)
Courbe ROC = graphique montrant le tracé des valeurs de la sensibilité en fonction de (1 - la spécificité) pour chaque valeur seuil donnée.
Le « point le plus discriminant » correspond à celui qui présente la SSC (surface sous la courbe) la plus élevée. Le point idéal est le coin supérieur gauche (spécificité = sensibilité = 1) à on choisit le point de la courbe le plus proche du coin supérieur gauche.
En pratique, on ne choisit pas toujours ce point : il peut être important de privilégier la spécificité (traitement très toxique,…) ou la sensibilité (maladie à évolution fatale rapide,…). On choisit alors un autre point sur la courbe.
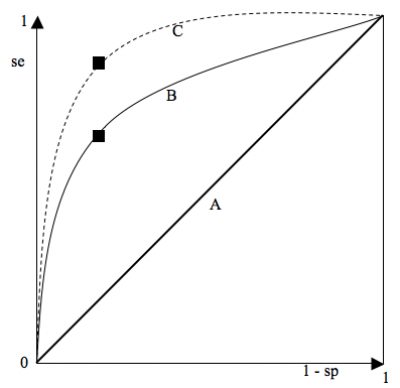
- Courbe A (diagonale d’égalité) : le meilleur point correspond à une sensibilité = spécificité = 0,5 à cette courbe correspond à un test totalement inefficace : il y a autant de gens sains déclarés malades que non malades et autant de gens malades déclarés sains que malades.
- Courbe B : correspond à la courbe de température comme test diagnostique pour la grippe. Le meilleur point correspond à une sensibilité = 0,65 et une spécificité = 0,75, valeurs déterminées pour un seuil de 39°C.
- Courbe C correspond à un test presqu’idéal, permettant d’obtenir des valeurs très élevées de spécificité et de sensibilité. Ex : dosage des CK et infarctus.
La courbe ROC offre donc une estimation globale de la valeur d’un séparateur et peut comparer la valeur discriminante de deux tests.
Approche bayesienne des essais cliniques versus approche fréquentiste
L'approche fréquentiste nécessite un p < 0,05. L'approche Bayesienne un p > 0,95.
La probabilité à priori est ici difficile à cerner, il s’agit plutôt d’une probabilité subjective (degré de croyance en l’efficacité du tt avant de l’évaluer). Elle peut s’assimiler à la fréquence moyenne des résultats positifs obtenus avec les essais thérapeutiques. La valeur prédictive dépend ici de la probabilité à priori (en cas de situation très spéculative où l’essai est réalisé sans qu’il y ait de justification à priori, elle est très faible (une proba à priori de 50% revient à adopter une approche fréquentiste simple traditionnelle) à la VP sera faible même en cas de résultat hautement significatif) mais aussi de la puissance de l’essai (augmente avec la puissance).
Pour un essai de phase III, la proba à priori d’efficacité est > 90% à la VPP d’un résultat significatif sera très importante.
La régression et la corrélation
Régression : l’analyse de régression est un outil pour étudier et mesurer la relation existant entre des variables
Variable dépendante : variable prédite Y par une ou plusieurs variables indépendantes X (= prédicteurs)
Variable(s) indépendante(s) : variable(s) X utilisées pour prédire la variable dépendante.
Estimation des paramètres d’une régression linéaire (en cas de variable dépendante continue) : Y= a + bX tel que b soit la pente (dY/dX) de la droite de régression et a l’interception avec l’axe des Y pour X=0. L’estimation se fait par la méthode des moindres carrés (minimiser le carré des distances par rapport à la droite
Corrélation : le coefficient de corrélation simple (r) est une mesure de l’intensité de la relation linéaire entre deux variables aléatoires. Il varie de -1 (pente négative -45°) à 1 (pente positive 45°), 0 indiquant l’absence de relation linéaire. (NB : une interprétation d’un r multiple est moins évidente)
- ! une corrélation significative n’indique pas forcément une relation causale ! Et s’il y a causalité, on n’en connaît pas le sens (savoir ce qui est la cause et l’effet relève de l’interprétation biologique).
- Une corrélation peut être faussement significative lorsque les 2 variables X et Y partagent la même variable (= couplage mathématique). Ex : transport et consommation d’O2 dépendent tous deux du débit cardiaque.
- r(X,Y) = covariance / produit des racines carrées des variances = Sxy/ √[Sx² x Sy²]
On peut tester la signification de r par comparaison avec 0 (absence de signification). On utilise le test :
t = (r/ √[1-r²] ) x √[n-2] tel que n-2 soit le d.d.l. avec n = nombre de couples (x,y). Ho : r = 0
! Pour s’assurer qu’un résultat soit significatif, il faut non seulement un p< 0,05 mais aussi que l’équation Y=a+bX ait un sens biologique, soit vraisemblable.
Une fois que l’on a déterminé la droite par la méthode des moindres carrés, on peut déterminer la bande de confiance à 95% (2 courbes entourant la droite) concernant la pente de la droite. On peut également déterminer la bande de prédiction à 95% (contenant 95% des points)
Coefficient de détermination r² : varie entre 0 et 1. Correspond au pourcentage des changements de y expliqués par x. Ex : Y : TAS, X : âge, r = 0,718, r² = 0,516 à 51,6% de la variation de la TAS s’explique par la variation de l’âge (48,4% expliqués par d’autres facteurs [obésité, pratique d’un sport, génet, tabagisme,…].
La régression linéaire multiple : son principe est de construire une équation avec plusieurs prédicteurs pour prédire une variable continue. Ex : prédire la TAS selon l’âge, le poids, le sexe,… Y = b0 + b1 X1 + b2 X2 +… tels que les b soient des paramètres (= coefficient de régression partielle) et les X les variables. Chaque coefficient peut alors faire l’objet d’un test qui, s’il est significatif, signifie que la variable y correspondant a une valeur pronostique pour Y. On peut calculer un r multiple et un r² multiple, ainsi qu’un r² ajusté.
La régression logistique repose sur le même principe que la régression linéaire mais est utilisable lorsque la variable dépendante Y est dichotomique (qualitative à deux niveaux = variable discrète, non continue). Ex : présence (1) ou absence (0) de coronopathies en fonction de l’âge. On utilise alors un graphes de proportions de coronopathies (donc une variable continue) en fonction de l’âge à sigmoïde, qu’on peut transformer en droite par la régression logistique, on obtient alors un graphe de logit (proportion) en fonction de l’âge.
Ex : le score APACHE (calculé à l’admission en USI pour prédire la mortalité en fonction de ce score et de l’affection dont souffre le patient) est calculé selon une équation de régression logistique multivariable.
Les études longitudinales de survie
Définitions
- Durée de survie = temps écoulé entre naissance et la mort. Dans ces études elle commence au début du diagnostic/ début du traitement (= date d’origine)
- Date des dernières nouvelles = date la plus récente où l’on a recueillie des renseignements sur la santé du patient
- Date de point = date choisie pour calculer la durée de survie
- Durée de surveillance = délai entre la date d’origine et la date des dernières nouvelles
- Durée de participation = délai entre la date d’origine et la date des dernières nouvelles ou la date de point (on prend la date la plus tardive).
- Statuts du patient :
- Perdu de vue : dont on ne connaît pas l’état de santé à la date de point (à source de perte d’infos et de biais)
- Exclu-vivant : sujet vivant à la date de point et après cette date
- Observations censurées = sujets perdu de vue et exclu-vivant
- Décédé : décès avant la date de point
Courbes de survie non paramétriques de Kaplan Meier
« Etre encore en vie après l’instant t, c’est être en vie juste avant l’instant t et ne pas mourir à l’instant t » [oui, bon...]
Pour estimer la fonction de survie S(t) d’une population à partir d’un échantillon de taille n, il faut classer les observations par ordre croissant de temps de participation. On définit :
- ti : les instants auxquels les décès sont observés
- ni le nombre de sujets en vie juste avant ti = nbre de sujets exposés au risque de décéder à ti
- mi le nombre de décès à ti
- ci le nombre de données censurées (perdus de vue et exclus-vivants) entre [ti et ti+1[
→ taux de décès instantané = nbre de décès dans l’intervalle / (nbre de sujets – nbre de censurés et de décédés au cours des périodes précédentes) à taux de survie pour la période à taux de survie globale.
On peut comparer deux courbes de survie grâce au test du Logrank (ex : pour un groupe traité et un groupe placebo)
Courbes de survie par la méthode actuarielle (Bohmer)
Différence avec la méthode de Kaplan : les probabilités conditionnelles sont estimées pour des intervalles de temps fixés à priori et non pas par les dates des décès observés
Courbes de survie par le modèle de Cox = régression de Cox (semi-paramétrique)
Permet la prise en compte simultanée de plusieurs variables pour expliquer la survie, sans donner aux fonctions de survie des formes paramétriques précises. à ajustement selon l’âge, le sexe,.. + permet l’identification des variables pronostiques pertinentes.
Egalement appelé modèle des risques proportionnels car il assume que chaque facteur affectant le risque l’affecte du même rapport à tout instant.